Формирование универсальных учебных действий
в технологии деятельностного подхода
(развивающего обучения Д.Б.Эльконина-В.В.Давыдова)
на уроках математики в основной школе
|
|
Павелкин В.Н. кандидат физико-математических наук; ведущий научный сотрудник отдела сопровождения ФГОС ИРО ПК |
Стандарты второго поколения предполагают переход с
объяснительного на системно-деятельностный метод
обучения, в основе которого лежит принцип самостоятельного открытия знаний на
основе рефлексивной самоорганизации - возникло затруднение, значит надо прекратить
действовать и начать думать. Использование технологии обеспечивает достижение
высоких результатов как в освоении знаний и навыков, так и в общем развитии
учащихся. На уроках с использованием данной технологии ребята учатся лучше
рассуждать, думать, анализировать, не бояться трудностей, самостоятельно решать
ставшие перед ними проблемы, ставить цели и их добиваться, быть творческими
личностями. Они учатся общаться, уважать мнение каждого и считаться друг с другом.
В общем на таких уроках дети учатся самостоятельно
учиться.
В соответствии со стандартом второго поколения умение
учиться представляет собой способность к универсальным учебным действиям.
При обучении в системно-деятельностном
режиме на уроках формируются все универсальные учебные действия (УУД) в
процессе освоение нового способа деятельности.
На первом этапе освоения нового способа учащимся
предлагаются задания на известный способ действия, затем проблемное задание,
находящееся в зоне ближайшего развития учащегося [1], так называемое задание
постановки учебной задачи [2]. Здесь формируется личностное УУД -- самоопределение, учащийся узнает границы своего знания.
При этом усиливается (или возникает) мотивация учебной деятельности (тоже
самоопределение), т.к. как же решается эта проблемная задача, если она так
похожа на те, что он недавно решал, но решить не может.
Следующий этап – формулирование проблемы, формируемые УУД:
анализ, постановка и решение проблем, выбор оснований и критериев для сравнения
(общеучебные УУД); смыслообразование
(личностные); построение речевых высказываний, формулировка вопроса (коммуникативные);
целеполагание (постановка учебной задачи на основе
соотнесения того, что уже известно и усвоено учащимися, и того, что ещё
неизвестно) (регулятивные)..
3 этап – решение проблемы в группах,
формируемые УУД: самоопределение, смыслообразование
(личностные); анализ с целью выделения признаков (существенных,
несущественных), синтез как составление целого из частей, восполняя недостающие
компоненты, установление причинно-следственных связей, построение логической
цепи рассуждений, доказательство, выдвижение гипотез и их обоснование,
самостоятельное создание способов решения проблем творческого и поискового
характера (общеучебные, познавательные); волевая саморегуляция в
ситуации затруднения, целеполагание (постановка
учебной задачи на основе соотнесения того, что уже известно и усвоено
учащимися, и того, что ещё неизвестно) (регулятивные); планирование
(определение цели, функций участников, способов взаимодействия), постановка
вопросов (инициативное сотрудничество в поиске и сборе информации), разрешение
конфликтов (выявление, идентификация проблемы, поиск и оценка альтернативных
способов разрешения конфликта, принятие решения и его реализация), управление поведением
партнёра точностью выражать свои мысли (коммуникативные).
4 этап – моделирование найденного
нового способа, формируемые УУД: абстрагирование, знаково-символические,
моделирование, подведение под понятие, выведение следствий (общеучебные);
смыслообразование (личностные); целеполагание
(постановка учебной задачи на основе соотнесения того, что уже известно и
усвоено учащимися, и того, что ещё неизвестно), планирование (определение
последовательности промежуточных целей с учётом конечного результата;
составление плана и последовательности действий) (регулятивные).
5 этап – решение различных частных задач на новый
способ, УУД: самоопределение (мотивация учения, формирование основ гражданской
идентичности личности), смыслообразования
(личностные); поиск выделение информации, анализ с целью
выделения признаков (существенных, несущественных), синтез как составление
целого из частей, восполняя недостающие компоненты, выбор оснований и критериев
для сравнения, сериации, классификации объектов,
подведение под понятие, выведение следствий, установление причинно-следственных
связей, построение логической цепи рассуждений, доказательство, самостоятельное
создание способов решения проблем творческого и поискового характера
(познавательные); если решение задач происходит в группах, то
формируются все коммуникативные УУД; целеполагание
(постановка учебной задачи на основе соотнесения того, что уже известно и
усвоено учащимися, и того, что ещё неизвестно), планирование (определение
последовательности промежуточных целей с учётом конечного результата;
составление плана и последовательности действий) (регулятивные).
6 этап – самоконтроль и коррекция нового способа, формируемые
УУД: анализ с целью выделения признаков (существенных, несущественных), синтез
как составление целого из частей, восполняя недостающие компоненты, выбор
оснований и критериев для сравнения, сериации,
классификации объектов, подведение под понятие, выведение следствий, установление
причинно-следственных связей, построение логической цепи рассуждений (познавательные),
постановка вопросов ( инициативное сотрудничество в
поиске и сборе информации), разрешение конфликтов ( выявление, идентификация
проблемы, поиск и оценка альтернативных способов разрешения конфликта, принятие
решения и его реализация) (коммуникативные); прогнозирование (предвосхищение
результата и уровня усвоения, его временных характеристик), контроль (в форме
сличения способа действия и его результата с заданным эталоном с целью
обнаружения отклонений и отличий от эталона), коррекция (внесение необходимых
дополнений и корректив в план и способ действия в
случае расхождения эталона, реального действия и его продукта) (регулятивные).
7 этап – оценка и самооценка, формируемые УУД:
самоопределение (мотивация учения, формирование основ гражданской идентичности
личности), смыслообразование ( «какое
значение, смысл имеет для меня учение», и уметь находить ответ на него),
нравственно-этического оценивания (оценивание усваиваемого содержания, исходя
из социальных и личностных ценностей, обеспечивающее личностный моральный
выбор) (личностные); анализ с целью выделения признаков (существенных,
несущественных), синтез как составление целого из частей, восполняя недостающие
компоненты, выбор оснований и критериев для сравнения, сериации,
классификации объектов (познавательные); постановка вопросов
(инициативное сотрудничество в поиске и сборе информации), разрешение
конфликтов (выявление, идентификация проблемы, поиск и оценка альтернативных
способов разрешения конфликта, принятие решения и его реализация), управление
поведением партнёра точностью выражать свои мысли (контроль, коррекция, оценка
действий партнёра умение с достаточной полнотой и точностью выражать свои
мысли) (коммуникативные), оценка (выделение и осознание учащимися того, что уже
усвоено и что ещё подлежит усвоению, осознание качества и уровня
усвоения), волевая саморегуляция (способность к
мобилизации сил и энергии; способность к волевому усилию – к выбору в ситуации
мотивационного конфликта и к преодолению препятствий) (регулятивные).
Необходимо отметить, что универсальные учебные
действия могут быть сформированы только при условии строгого следования
принципам системно-деятельностного подхода (СДП),
один из вариантов реализации которого (наиболее эффективный, по моему мнению),
представлен выше. Одни и те же задания могут формировать УУД в ситуации реализации
принципов СДП, в ситуации нарушения принципов СДП никаких УУД может и не
сформироваться. Например, логические УУД формируются только при условии, что
предлагаемые задания учащийся видит впервые, подобные задания не были решены
учителем и т.д. Можно даже сформулировать теорему: УУД на уроках математики (думаю
и не только) формируются лишь в режиме системно-деятельностного
подхода к обучению. Все перечисленные этапы необходимы для успешного
самостоятельного освоения новых знаний, способов деятельности. И только в
процессе такого режима учебной деятельности учащиеся развивают свои способности
к учению.
При таком обучении (СДП) для каждой темы, т.е. нового
способа деятельности, очень важным является наличие заданий, расположенных в
определенной последовательности, которая соответствует технологии СДП. Новая
тема должна начинаться с заданий, формирующих ситуацию успеха. Эти задания на
зону актуального развития должны быть знакомы учащимся с одной стороны, а с
другой стороны, они должны содержать все необходимое для построения нового
способа. Т.е. содержание этих известных способов должно подвести учащихся к
решению основной проблемы новой темы. Следующее задание – так называемое
«задание постановки учебной задачи», в нем должна содержаться проблема, решение
которой выводит на новый способ. Далее задания на преобразование и уточнение
нового способа, задания моделирования и задания на применение его в различных
учебных ситуациях.
Приведем несколько проектов уроков постановки учебной
задачи (этапы 1 и 2), математика 5 класса, в каждом из которых приведена
необходимая последовательность заданий.
Проект урока
"Сравнение дробей с одинаковыми знаменателями"
Урок
1
Тип
урока: постановка учебной задачи
Формируемые
УУД:
Личностные
Самоопределение (мотивация учения)
Познавательные
- формулирование познавательной цели;
- поиск и выделение информации;
- анализ с целью выделения признаков (существенных,
несущественных)
- формулирование проблемы;
- самостоятельное создание способов решения проблем
творческого и поискового характера.
Коммуникативные (групповая
работа)
Планирование (определение цели, функций участников,
способов взаимодействия).
Постановка вопросов (инициативное сотрудничество в
поиске и сборе информации).
Этапы урока
I Ситуация успеха (фронтальный опрос)
II Проблемная ситуация и анализ проблемы (групповая
работа)
III Обсуждение
выдвинутых гипотез.
I
1)
Приведите примеры
обыкновенных дробей.
2)
Из чего состоит
дробь?
3)
Где стоит
знаменатель, что он показывает?
4)
Где стоит
числитель, что он показывает?
5)
Что означают
дроби ![]() ?
?
6)
Запишите дробь,
описывающую заштрихованную часть квадрата [3, 4] на рисунках 1 и 2:
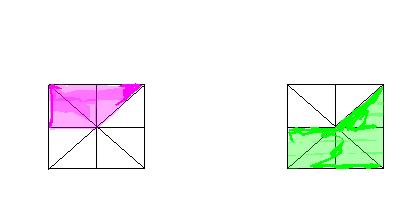
Рис. 1 Рис 2
7)
Отметьте на
числовой оси число ![]() .
.
![]()
II Задание постановки учебной задачи
Выберите пары дробей, в которых вы можете произвести
сравнение дробей. Ответьте, почему вы сделали такой выбор?
![]() и
и ![]() ,
,
![]() и
и ![]() ,
,
![]() и
и ![]() ,
,
![]() и
и ![]() ,
,
![]() и
и ![]() .
.
б) Сравните дроби в выбранных парах и обоснуйте ответ.
Формулирование и анализ проблемы. Работа в группах.
Обсуждение групповых версий
Задание
моделирования нового способа действия.
Сформулируйте правило сравнения дробей с равными
знаменателями.
Задачи на
найденный способ действия
1.
Продолжительность
урока 40 мин., на решение задачи ушло 7 мин., на проверку домашнего задания
ушло 10 мин., а остальное время – на проведение самостоятельной работы. Какая
часть урока ушла на а) решение задачи; б) проверку домашнего задания; в)
самостоятельную работу. Сравните полученные дроби и поставьте их в порядке
возрастания.
2.
При каких
значениях неизвестных неравенства будут верными:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.
Игра «Счастливый
случай»
Правила: 1 команда называет любую дробь, вторая
называет любую большую названной дробь и т.д. Выигрывает та команда, которая
объясняет, что игра бесконечная.
Домашнее задание:
1.
Придумать сказку,
стихотворение или загадку, где используется правило сравнения дробей.
Проект урока
постановки учебной задачи
Тема:
Основное свойство дроби
Цели и задачи:
1.
Организовать
исследовательскую деятельность направленную на
построение понимания понятия основного свойства дроби
2.
Конкретизировать
понятие основного свойства дроби и задать зону ближайшего развития на
приведение дробей к общему знаменателю и дальше: сравнению, сложению, вычитанию
дробей с разными знаменателями
3.
Способствовать
продвижению учеников в общем развитии
Формируемые
УУД:
Личностные
Самоопределение (мотивация учения)
Познавательные
- формулирование познавательной цели;
- поиск и выделение информации;
- анализ с целью выделения признаков (существенных,
несущественных)
- формулирование проблемы;
- самостоятельное создание способов решения проблем
творческого и поискового характера.
Коммуникативные (групповая
работа)
Планирование (определение цели, функций участников,
способов взаимодействия).
Постановка вопросов (инициативное сотрудничество в
поиске и сборе информации).
1.
Ситуация успеха
Зона актуального развития:
·
Ученики отмечают
дробные, смешанные, целые числа на числовом луче
·
Знают определение
дроби
·
Сформулированы
понятия НОК и НОД
1)
Отметьте на числовом луче точки ![]()
Чему равно расстояние от 0 до точек.
2) Сравните дроби (как вариант: рассмотрите пары
дробей, выделите лишнюю)
а) ![]() б)
б) ![]() в)
в) ![]()
г) ![]() д)
д) ![]()
Две последние пары дробей вызывут
затруднения у ребят, т.к. пары под а), б), в) изображены на числовом луче, а г)
и д) – нет – возникает проблемная ситуация –
необходимость вывода какого-то способа, закономерности.
В ходе обсуждения версий ребята выделяют равные дроби
под буквами а – г, выделяют закономерность, задаются
вопросом почему? Т.о. выходят на предположение, что если знаменатель и числитель
дроби умножить или разделить на одно и то же число, то получится равная ей
дробь.
2.
№ 238 (учебник
Математика-5, автор Ванцян [5])
1.
Подставь вместо
звездочки нужное число
![]()
![]()
![]()
Каким свойством дроби ты при этом пользовался?
2.
Выпиши из чисел
16, 42, 24, 166, 20, 32, 144 те которые могут быть знаменателем дроби, равной ![]() . Объясни свой выбор и запиши эти дроби.
. Объясни свой выбор и запиши эти дроби.
3.
Какие из
приведенных в пункте 2 чисел могут быть числителем дроби, равной ![]() ? Почему? Запиши эти дроби.
? Почему? Запиши эти дроби.
4.
Выбери из чисел
21, 40, 64, 35, 96, 10, 84, 24 те, которые могут быть числителем и знаменателем
дробей, равных ![]() . Запиши эти дроби.
. Запиши эти дроби.
Обобщение опыта и конкретизация ![]()
3.
Рефлексия
Почему 45 мин. – три четверти часа
20 мин. – треть часа
Ловушка: Запиши несколько дробей равных данным изменив
числитель и знаменатель дроби как в сторону увеличения
так и в сторону уменьшения.
а) ![]() ; б)
; б) ![]() .
.
Подчеркивается важность полученного способа
превращения (преобразования) дробей, дальше варианты:
1)
сразу назвать
основным и после введения операций сложения и вычитания и сравнения дробей с
разными знаменателями подчеркнуть происхождение названия основного.
2)
Не называть его
основным сразу, а только после того как еще раз подчеркнув важность свойства в
обозначении в темах сложения, вычитания и сравнения, сказать, что оно основное
4.
Домашнее задание
№235 из учебника А.Г.Ванцяна
[5]
Запишите еще две дроби, чтобы равенство было верным
(постарайтесь сделать вывод)
![]()
Список литературы:
1. Программа «Учусь
учиться» курса математики для 5-6 классов средней школы по образовательной системе
деятельностного метода обучения «Школа 2000…», М.:
ACADEMIA АПКиППРО,
2. В.В.Давыдов Теория развивающего обучения. – М.: ИНТОР, - 1996. – 544 с.
Г.В.Дорофеев, Л.Г.Петерсон. Математика. 6 класс. Часть 1,2,3.– М.: Ювента,2008 г.
3. Математика 5-6 классы. Методические
материалы к учебникам Г.В.Дорофеева, Л.Г.Петерсон. –
М, : Ювента,
4. А.Г.Ванцян.
Математика 5 кл. Учебно-методический комплект
"Математика. 5 класс" (вместе с рабочими тетрадями в 4 частях и
методическим пособием для учителя) создан с целью продолжения обучения
математике по системе общего развития Л. В. Занкова в
среднем звене общеобразовательной школы. М.: Издательство Федоров,
